Geometrias

Geometrias fractais

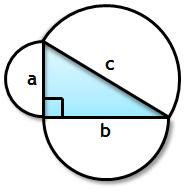
Os gregos antigos desenvolveram uma geometria de linhas e círculos, de régua e compasso, onde o rei era o triângulo rectângulo e o teorema de Pitágoras o seu representante. Durante dois milénios, a platónica pureza da geometria grega fez as delicias de agrimensores e poetas.

Um dia, enquanto descansava de não fazer nada na sua estufa, monsieur Descartes fixou a sua atenção na mosca que passeava pelo tecto. Para localizá-la inventou os sistemas de coordenadas, e com eles a geometria tornou-se analítica, tornou-se número, e abriu-se às mais estranhas fórmulas. E os engenheiros foram felizes.

Mas não aqueles matemáticos, que sempre olharam de lado o quinto axioma de Euclides. Por fim os mais ousados renegaram o axioma da paralela única e inventaram as geometrias não euclidianas. Com elas o espaço fez-se curvo e os físicos reinventaram o universo.

Contudo, a geometria nunca pôde modelar a forma das nuvens ou dos fetos, nem a disposição das montanhas, nem a formação das plantas, animais e seres humanos. Até que chegou Mandelbrot, que revelou a rugosidade do real e deu nome a uma nova forma de olhar: chamou-lhe geometria fractal.

Os fractais são formas rugosas que preenchem o vazio tão densamente que alcançam dimensões superiores às da linha ou da superfície: retorcem-se para preencher cada nicho, cada meandro do espaço, fazem-no copiando-se a si próprias em distintas e incessantes escalas. É graças a esta característica, a auto semelhança, que os fractais se adaptam tão bem à representação de certas formas naturais. Mas há mais, porque os fractais não são somente objectos científicos ou técnicos, são também estéticos, que é possível explorar graças a esta janela que é o monitor do computador. Mas isso já é outra história...

Traduzido de Epsilones

Geogebra

Dei-me agora conta de que para conseguirem abrir os ficheiros em Geogebra anexados a esta página, têm que instalar o Geogebra no vosso computador.

Isso é simples, já que este programa de Geometria Dinâmica é freeware (grátis às Damas e ... aos Cavalheiros, também) e podem descarregá-lo aqui.

Uma aplicação (interactiva) do Teorema de Pitágoras

A que distância vês o horizonte?
Clica aqui!

(Ficheiro obtido a partir de Geometría Dinámica).

"Pit" no espaço!

E o Teorema de Pitágoras no espaço?
Alguém quer contribuir?...

Aqui vai uma contribuição. E mais outra.

(Ficheiros obtidos a partir de Geometría Dinámica).

O Teorema de Pitágoras III

Demonstração do teorema de Pitágoras generalizado

O surpreendente é que a relação estabelecida pelo Teorema de Pitágoras se pode generalizar a todo terno de figuras semelhantes cujos comprimentos formem um terno pitagórico. Se em vez três aborrecidos quadrados desenharmos sobre um triângulo rectângulo três gatos de Cheshire, a área da superfície ocupada pelo desenho do maior dos três será igual à soma das áreas dos outros dois desenhos.

A demonstração deste facto é praticamente trivial:

Seja a um comprimento qualquer do gato grande (pode ser a sua largura, mas também a distância entre os extremos das orelhas, ou a amplitude do seu sorriso). Sejam b e c os mesmos comprimentos mas medidos nas outras duas imagens, b para o gato médio e c para o pequeno. a, b e c formam um terno pitagórico, ou seja, cumprem:

a^2 = b^2 + c^2 [1]

Sejam A, B e C as áreas das superfícies ocupadas pelo desenho de cada um dos gatos, do maior ao menor. É sabido que se duas figuras são semelhantes, o quociente entre as suas áreas é igual ao quadrado do quociente entre os seus comprimentos.

Portanto: B/A = (b/a)^2 , C/A = (c/a)^2

Simplificando: b^2 = a^2. B/A, c^2 = a^2. C/A

Substituindo em [1], vem: a^2 = a^2. B/A + a^2. C/A

Simplificando: A = B + C.

A partir de Epsilones

Para além do teorema de Pitágoras - II

As lúnulas e o triângulo

Seja [ABC] um triângulo rectângulo. Tracemos o semicírculo circunscrito ao triângulo, e os dois semicírculos de diâmetros [AB] e [AC] exteriores ao triângulo. A soma das áreas das lúnulas assim obtidas é igual à área de outra das superfícies que se vêm na figura. De que superfície se trata?
Nota: as medidas concretas do triângulo não importam. Não se trata de fazermos contas e procurarmos alguma coincidência.


Solução:

A soma das áreas das lúnulas coincide com a área do triângulo [ABC].

Uma variante

A terceira linha do desenvolvimento anterior é na realidade una demonstração do teorema de Pitágoras para semicírculos. Dando por sabido o teorema de Pitágoras generalizado, a demonstração fica assim:

Seja L a área das lúnulas:

L = b + c + d - a

Pelo teorema de Pitágoras generalizado,

a = b + c

Então

L = b + c + d - (b + c)

L = d

A partir de Epsilones

Um passo para além do Teorema de Pitágoras

Embora o Teorema de Pitágoras esteja por aí há milhares de anos, a variedade de provas e de ideias que dele decorrem continuam a fascinar-nos. Há várias formas de enunciar o teorema.

Por exemplo:
Dado um triângulo rectângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

ou - Dado um triângulo rectângulo, a soma das áreas dos dois quadrados construídos a partir dos catetos desse triângulo é igual à área do quadrado construído a partir da hipotenusa desse triângulo.
(Ver aqui e aqui duas demonstrações interactivas do Teorema de Pitágoras em Geogebra).

Agora, descubramos uma variação desta última forma. Suponhamos que em vez de somarmos as áreas dos quadrados construídos nos catetos e na hipotenusa, somamos as áreas de outras figuras geométricas semelhantes, e verifiquemos se o teorema ainda continua verdadeiro. Resultará sempre para objectos semelhantes?


Área do círculo A = (1/2).(a/2)^2.pi = (a^2.pi)/4
Área do círculo B = (1/2).(b/2)^2.pi = (b^2.pi)/4
Área do círculo C = (1/2).(c/2)^2.pi = (c^2.pi)/4

E, comparando as suas áreas vem:
(a^2+b^2).pi/4 = c^2.pi/4

Traduzido de "More joy of Mathematics" de Theoni Pappas

E para gatos?! :-)
O gato da "Alice no país da maravilhas" de Lewis Carroll (pseudónimo do escritor e matemático Inglês, Charles Lutwidge Dodson).