Um passo para além do Teorema de Pitágoras

Embora o Teorema de Pitágoras esteja por aí há milhares de anos, a variedade de provas e de ideias que dele decorrem continuam a fascinar-nos. Há várias formas de enunciar o teorema.

Por exemplo:
Dado um triângulo rectângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

ou - Dado um triângulo rectângulo, a soma das áreas dos dois quadrados construídos a partir dos catetos desse triângulo é igual à área do quadrado construído a partir da hipotenusa desse triângulo.
(Ver aqui e aqui duas demonstrações interactivas do Teorema de Pitágoras em Geogebra).

Agora, descubramos uma variação desta última forma. Suponhamos que em vez de somarmos as áreas dos quadrados construídos nos catetos e na hipotenusa, somamos as áreas de outras figuras geométricas semelhantes, e verifiquemos se o teorema ainda continua verdadeiro. Resultará sempre para objectos semelhantes?


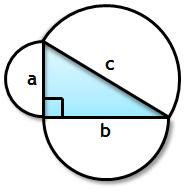
Área do círculo A = (1/2).(a/2)^2.pi = (a^2.pi)/4
Área do círculo B = (1/2).(b/2)^2.pi = (b^2.pi)/4
Área do círculo C = (1/2).(c/2)^2.pi = (c^2.pi)/4

E, comparando as suas áreas vem:
(a^2+b^2).pi/4 = c^2.pi/4

Traduzido de "More joy of Mathematics" de Theoni Pappas

E para gatos?! :-)
O gato da "Alice no país da maravilhas" de Lewis Carroll (pseudónimo do escritor e matemático Inglês, Charles Lutwidge Dodson).